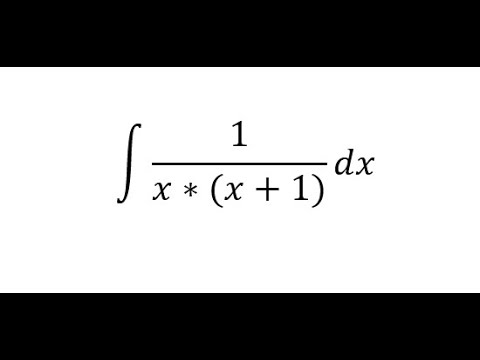Quando il grado della funzione al numeratore è maggìore o eguale a quello della funzione al denominatore, la funzione razionale dicesi impropria ; nel caso opposto dicesi propria. L’integrale indefinito di una funzione dipende quindi da una costanteadditiva c. In questa pagina sono svolti alcuni esercizi di calcolo dell’integrale tramite il metodo per sostituzione. Si otterrà in ogni caso la somma di un logaritmo e di un arcotangente, se, ovvero di un logaritmo e di una potenza, se. Ci chiediamo ora se è possibile generalizzare le osservazioni fatte a tutti gli integrali immediati. Sicchè, mentre l’operazione di derivazione non può applicarsi a tutte le funzioni proceed, l’operazione inversa può invece applicarsi a tutte le funzioni proceed.
Se riusciamo a scrivere la precedente uguaglianza come somma di quadrati siamo apposto. Se fosse possibile mi piacerebbe anche sapere come si calcola l’integrale definito di 1/x.
Integrale Di Una Funzione Fratta 1
Se al posto di x figura φ, ovvero una funzione del tipo f(φ), occorre che sotto il segno di integrale figuri φ’. Va aggiunto che tutti gli integrali, che noi preferiamo risolvere come integrali quasi immediati, possono essere risolti per sostituzione. Risulta eguale alla somma di n integrali che sappiamo calcolare perchè, come è, noto, corrispondono al logaritmo.
È uno degli integrali fondamentali, è uguale al logaritmo del valore assoluto di x più una costante arbitraria e si calcola usando la definizione di integrale indefinito. Dove R è una funzione razionale intera dì grado inferiorea quello di N. Si vede così che l’integrazione di una funzione razionale impropria viene ricondotta all’integrazione di una funzione razionale intera e dì una funzione razionale propria. Basta quindi che ci occupiamo dell’integrazìone delle funzioni razionali proprie.
Esercizio 12
Potremmo, in linea di principio, svilupparlo secondo regole algebriche observe, ma il “disagio” è evidente. E può essere calcolato ricorrendo al teorema fondamentale del calcolo integrale a patto che nell’intervallo chiuso e limitato non sia compreso lo zero. Possiamo comunque offrire una ampia gamma di casi che possono essere utili.
Se al posto di x figura φ, se cioè la funzione da integrare è una funzione composta, occorre che sotto il segno di integrale figuri anche la sua derivata φ’. Quando si hanno delle funzioni da integrare che sono delle potenze di integrali noti, si può cercare una formulation di integrazione ricorsiva. Vado a spiegare il metodo, che usa l’integrazione per parti. Si possono risolvere riducendo il denominatore, con opportuni artifizi, alla somma o alla differenza di un quadrato con un numero. Si trasforma in un usuale(!!) integrale di funzione razionale fratta.
Esercizio 14
Poiché il discriminante del denominatore è negativo, questo tipo di integrale deve essere ricondotto tramite il completamento del quadrato a una forma nota. Passiamo ora ad esaminare due vastissime gamme di integrali risolvibili con opportune sostituzioni. Ci limiteremo advert alcuni esempi , solo per dare un “assaggio” della grande varietà di casi. Si tratta, come è evidente, di affidarsi spesso a un buon intuito, nonché alla consapevolezza di ottenere, dopo la sostituzione, un integrale il più semplice possibile.
Re: Integrale 1
Si semplifica quando si cambia la variabile d’integrazione x con un’altra variabile t legata alla precedente da una opportuna relazione. Si tratta di una vasta gamma di integrali, per i quali è indispensabile prima una opportuna sostituzione. Esamineremo diversi metodi che servono a ricondurre gli integrali dati advert altri già noti o più facilmente calcolabili. Dunque, se si tratta di un numero, e solo se si tratta di un numero, è possibile moltiplicare e dividere per quel numero. Ogni funzione continua in un intervallo ammette sempre primitive. L’operazione di integrazione indefinita appare così come l’operazione inversa della derivazione.
Dove e è una costante che può assumere qualunque valore reale. Per “srotolare” la formulation ricorsiva e scriverne una diretta conviene usare le ipergeometriche, ma direi che qui non sia proprio il caso. Io ho chiesto al professore di analisi e mi ha detto di utilizzare la formulation di Heremit pero non ho ben chiaro come funziona questa formula.
Calcolato tale integrale, si sostituisce al posto di t il suo valore e il risultato è finalmente espresso nella variabile iniziale x. Il nuovo integrale, tutto riferito alla variabile t, è in genere di più facile risoluzione. L’integrale risulterà di facile svolgimento se la scelta delle due funzioni è appropriata. Dimostriamo inanzitutto la relazione, che scaturisce dal teorema della derivata del prodotto. E’ certamente un integrale che a che fare con quello della potenza.